Efficient Programming

R Programming

Ella Kaye and Heather Turner

Department of Statistics, University of Warwick

March 18, 2024

Overview

Memory management
Benchmarking
Improving run time
Parallelisation
Outlook to package development

Memory management

Overview

Objects created in R are stored in memory. This has the advantage that objects can be accessed faster, but R slows down as the memory fills up. Creating objects also takes time.

Therefore:

Re-use temporary variables. The allocated storage will be re-used if the vector has the same length.
Save results for re-use, e.g. index variables
Don’t save intermediate results unnecessarily – compute on-the-fly
Remove large objects when no longer needed (with rm())

Basic data structures

Try to use the simplest data structure for your purpose

matrices vs. data frames
character or integer vectors vs. factors
logical or integer vectors vs. numeric vectors
unnamed objects vs. named objects

It is especially important to use low-level structures for computation

You can create richer objects as a final step before returning to the user.

Big Data

Modern computers have enough RAM to work with millions of records using standard functions.

Some packages to work more efficiently with big data:

data.table faster operations on data frames; read/write large CSVs
dplyr + dbplyr processing of data in databases.
arrow read/write large CSVs or binary files e.g. Parquet; processing larger-than-memory data with dplyr commands.
bigmemory, biganalytics faster matrix operations, generalized linear models, kmeans

Growing Objects

Adding to an object in a loop

res <- NULL
for (i in 1:5000) res <- c(res, 1)

may force a copy to be made at each iteration, with each copy stored until the loop has completed.

It is far better to create an object of the necessary size first

res <- numeric(5000)
for (i in seq_along(res)) res[i] <- 1

To initialise a list we can use

res <- vector(mode = "list", length = 100)

Copy-on-Change

R usually copies an object to make changes to it.

tracemem can be used to trace copies of an object

z <- NULL
for (i in 1:3){ z <- c(z,1); print(tracemem(z)) }

[1] "<0x122220648>"
[1] "<0x11940ba08>"
[1] "<0x127b9b9c8>"

z <- numeric(2); print(tracemem(z))

[1] "<0x1193ce2c8>"

for (i in 1:2){ z[i] <- i;print(tracemem(z)) }

tracemem[0x1193ce2c8 -> 0x135159648]: 
[1] "<0x135159648>"
[1] "<0x135159648>"

Benchmarking

There will usually be many ways to write code for a given task. To compare alternatives, we can use benchmark the code.

If the code is more than a single expression, create wrappers for each alternative

grow <- function(n){
  res <- NULL
  for (i in 1:n) res <- c(res, 1)
  res
}
pre_specify <- function(n){
  res <- numeric(n)
  for (i in seq_along(res)) res[i] <- 1
  res
}

`bench::mark()`

Run the two alternatives with bench::mark(). This function

Runs alternatives ≥ 1 time; at most enough times to take 0.5s
Makes sure the two expressions return the same result!

library(bench)
(bm <- bench::mark(grow(5000), pre_specify(5000)))

Warning: Some expressions had a GC in every iteration; so filtering is
disabled.

# A tibble: 2 × 6
  expression             min   median `itr/sec` mem_alloc `gc/sec`
  <bch:expr>        <bch:tm> <bch:tm>     <dbl> <bch:byt>    <dbl>
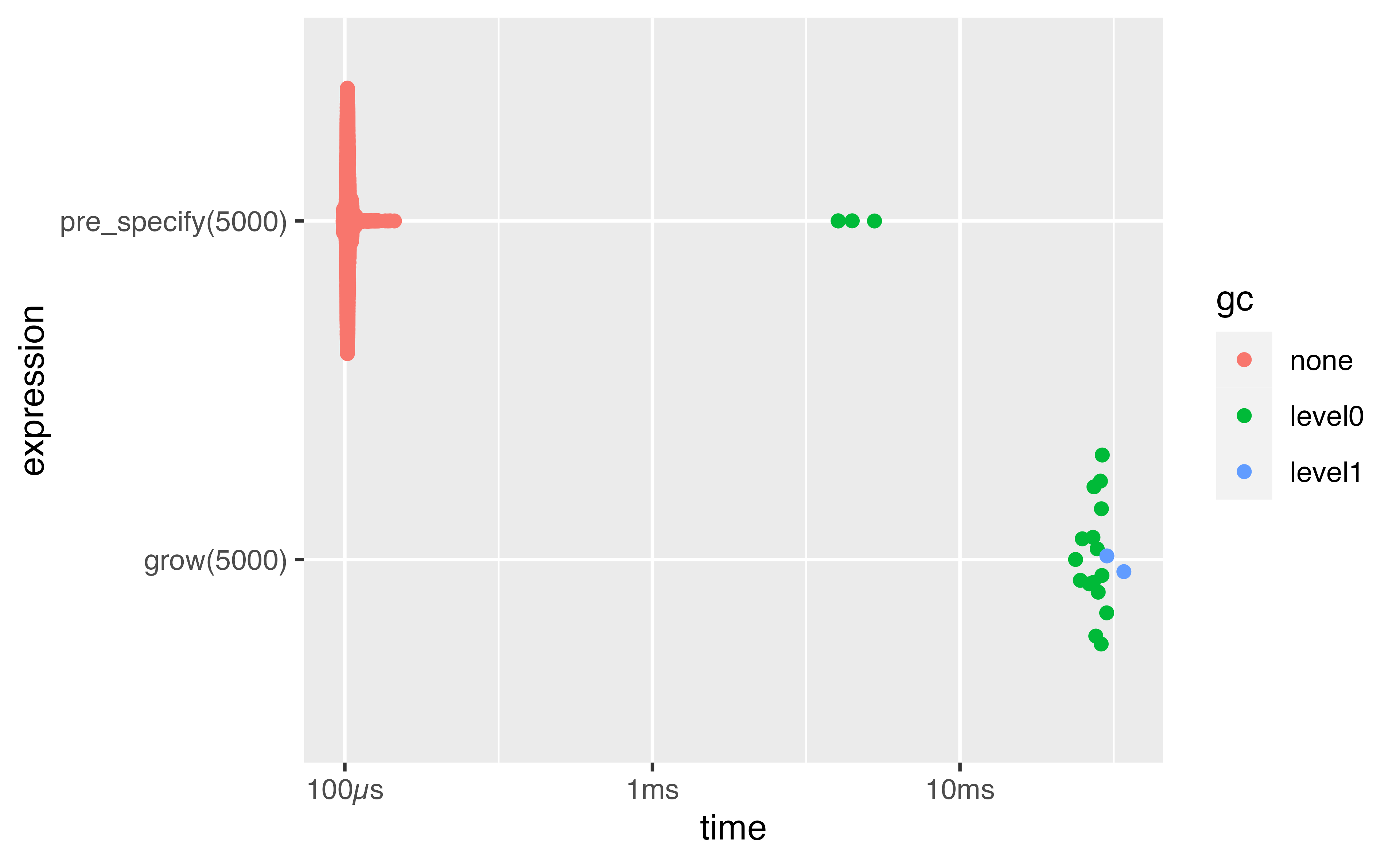
1 grow(5000)          23.8ms     28ms      35.8    95.6MB    65.6 
2 pre_specify(5000)   98.7µs    102µs    9362.     55.8KB     8.00

GC is the garbage collector which tidies up deleted objects
itr/sec is how many times the expression could be run in 1s

Plotting benchmarks

Distribution tends to be right-skewed - focus on the median!

plot(bm)

Scaling

Benchmarking can be difficult as the best option can depend on the size of the data, e.g. memory allocation can overshadow run time for small objects.

When thinking about how our code scales to bigger, we need to consider what we mean by “big”

number of rows or number of columns?
number of observations or number of factor levels?

bench::press() compares a function over a grid of parameters

`bench::press()`

bench::press(n = c(10, 100), k = c(10, 1),
  bench::mark(gl(n, k, length = 1000)) # `gl` generates factor levels
)

Running with:
      n     k

1    10    10

2   100    10

3    10     1

4   100     1

# A tibble: 4 × 8
  expression                  n     k    min median `itr/sec` mem_alloc `gc/sec`
  <bch:expr>              <dbl> <dbl> <bch:> <bch:>     <dbl> <bch:byt>    <dbl>
1 gl(n, k, length = 1000)    10    10 3.12µs 3.65µs   245179.    12.4KB     24.5
2 gl(n, k, length = 1000)   100    10 8.86µs 9.43µs   101218.   11.05KB     20.2
3 gl(n, k, length = 1000)    10     1 2.83µs 3.16µs   302419.    3.95KB     30.2
4 gl(n, k, length = 1000)   100     1  5.9µs 6.48µs   146617.    7.53KB     14.7

Exercise 1

Suppose we have a matrix of data and a two-level factor

nr <- 10
nc <- 50
X <- matrix(rnorm(nr * nc, 10, 3), nrow = nr)
grp <- gl(2, nc/2)

Use bench::mark() to compare the following ways to find the coefficients of a linear model fitted to each row

# one
res <- vector("list", nr)
for(i in seq_len(nr)){
  res[[i]] <- coef(lm(X[i,] ~ grp))
}
do.call("cbind", res)
# two
res2 <- coef(lm(t(X) ~ grp))

Improving run time

Faster common operations

Sorting
- Use sort(x, partial = 1:10) to get the top 10
- Use sort(x, decreasing = TRUE) vs rev(sort(x))

Generating numeric vectors
- seq.int(), seq_along(x), seq_len(n) vs seq()
- rep.int() or rep_len(n) vs rep()

which.min(), which.max() vs e.g. which(x == min(x))

anyNA(x) vs any(is.na(x))

For loops

For loops are an intuitive way to write code, but can be very inefficient.

for is a function, : or seq_along is another function, each use of [ is a call to a function, …, so a loop involves many nested function calls.

Try to keep for loops for truly iterative computations or tasks that are fast in any case (optimizing code takes time!)

Otherwise make loops as lean as possible, by pre-computing values that do not need be be computed iteratively.

Vectorization

Vectorization is operating on vectors (or vector-like objects) rather than individual elements.

Many operations in R are vectorized, e.g.

x <- 1:3
y <- 3:1
x == y

[1] FALSE  TRUE FALSE

log(x)

[1] 0.0000000 0.6931472 1.0986123

res <- list(a = 1:3, b = 1:6)
lengths(res)

a b 
3 6

We do not need to loop through each element!

Recycling

Vectorized functions will recycle shorter vectors to create vectors of the same length

1:4 + 0:1 + 2 # 1+0+2, 2+1+2, 3+0+2, 4+1+2

[1] 3 5 5 7

This is particularly useful for single values

cbind(1, 3:4)

     [,1] [,2]
[1,]    1    3
[2,]    1    4

and for generating regular patterns

paste0(rep(1:3, each = 2), c("a", "b"))

[1] "1a" "1b" "2a" "2b" "3a" "3b"

`ifelse()`

ifelse is a vectorised version of if and else blocks

x <- c(5, 2, 9, 12)
ifelse(x > 6, 2 * x, 3 * x)

[1] 15  6 18 24

Recycling is also very useful here

x <- 1:10
ifelse(x %% 2 == 0, 5, 12)

 [1] 12  5 12  5 12  5 12  5 12  5

However indexing is more efficient than ifelse

y <- rep.int(12, 10)
y[x %% 2 == 0] <- 5
y

 [1] 12  5 12  5 12  5 12  5 12  5

Logical operations

Logical operators such as & and | are vectorized, e.g.

x <- c(1, 0.6, 1.2, 0.4, 0.5)
x > 0.4 & x < 0.8

[1] FALSE  TRUE FALSE FALSE  TRUE

If we only want to compare vectors of length 1 the operators && and || are more efficient as they only compute the RHS if needed

x[1] > 0.4 && x[1] < 0.8

[1] FALSE

Make sure the vectors are of length 1, otherwise you get an error. This change was introduced in R ≥ 4.3.

x > 0.4 && x < 0.8

Error in x > 0.4 && x < 0.8: 'length = 5' in coercion to 'logical(1)'

Vectorization and Matrices

Vectorizations applies to matices too, not only through matrix algebra

M <- matrix(1:4, nrow = 2, ncol = 2)
M + M

     [,1] [,2]
[1,]    2    6
[2,]    4    8

but also vectorized functions

M <- M + rep(1.3, 4)
round(M)

     [,1] [,2]
[1,]    2    4
[2,]    3    5

Matrices and recycling: rows

Values are recycled down matrix, which is convenient for row-wise operations

M <- matrix(1:6, nrow = 2, ncol = 3)
M

     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

M - 1:2

     [,1] [,2] [,3]
[1,]    0    2    4
[2,]    0    2    4

Matrices and recycling: columns

To do the same for columns we would need to explicitly replicate, which is not so efficient.

M - rep(1:3, each = 2)

     [,1] [,2] [,3]
[1,]    0    1    2
[2,]    1    2    3

`apply()`

apply provides a way to apply a function to every row or column of a matrix

M <- matrix(1:20, 2, 10)
M

     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,]    1    3    5    7    9   11   13   15   17    19
[2,]    2    4    6    8   10   12   14   16   18    20

# MARGIN 1 over rows
apply(M, 1, quantile, 0.75)

[1] 14.5 15.5

# MARGIN 2 over columns
apply(M, 2, mean)

 [1]  1.5  3.5  5.5  7.5  9.5 11.5 13.5 15.5 17.5 19.5

`lapply()`

lapply applies a given function to each element of a list

l <- list()
l$x <- 1:3
l$y <- 4:6
lapply(l, mean)

$x
[1] 2

$y
[1] 5

`sapply()` and `vapply()`

sapply acts similarly to lapply, but tries to simplify the result

sapply(l, mean)

x y 
2 5

It is better to use vapply() in programming as it ensures the returned object is of the expected type (and is slightly faster)

vapply(l, mean, numeric(1))

x y 
2 5

Row/Column-wise Operations

Several functions are available implementing efficient row/column-wise operations, e.g. colMeans(), rowMeans(), colSums(), rowSums(), sweep()

M <- matrix(1:4, nrow = 2, ncol = 2)
rowMeans(M)

[1] 2 3

These provide an alternative to iterating though rows and columns in R (the iteration happens in C, which is faster).

The matrixStats provides further “matricised” methods, including medians and standard deviations.

Exercise 2 (h/t Raju Bhakta)

Sampling from 0.3 × N(0, 1) + 0.5 × N(10, 1) + 0.2 × N(3, 0.1):

# Set the random seed and the number of values to sample
set.seed(1); n <- 100000                 

# Sample the component each value belongs to
component <- sample(1:3, prob = c(0.3, 0.5, 0.2), 
                    size = n, replace = TRUE)

# Sample from the corresponding Normal for each value
x <- numeric(n)
for(i in seq_len(n)){
  if (component[i] == 1){
    x[i] <- rnorm(1, 0, 1)
  } else if (component[i] == 2) {
    x[i] <- rnorm(1, 10, 1)
  } else {
    x[i] <- rnorm(1, 3, sqrt(0.1))
  }
}

Exercise 2 (continued)

The for loop in the previous code is suitable for vectorization: the iterations are completely independent.

rnorm() is vectorized in the arguments mu and sd, e.g. to simulate a value from the 1st and 3rd component we could write:

mu <- c(0, 10, 3)
sd <- sqrt(c(1, 1, 0.1))
rnorm(2, mu[c(1, 3)], sd[c(1, 3)])

[1] -1.371225  3.324096

Use this information to replace the for loop, using a single call to rnorm() to simulate n values from the mixture distribution.

Use bench::mark() to compare the two approaches - don’t forget to set the same seed so the simulations are equivalent!

Parallelisation

Most functions in R run on a single core of your machine. The future.apply package, part of the futureverse, provides parallel versions of all the apply-type functions.

https://www.futureverse.org

Parallelisation is most straight-forward to implement for embarrassingly parallel problems, such as applying a function to elements of a list.

Example setup

Adapted from https://henrikbengtsson.github.io/course-stanford-futureverse-2023/

Let’s create a slow function:

slow_sum <- function(x) {
  sum <- 0
  
  for (value in x) {
    Sys.sleep(0.5)  ## half-second slowdown per value
    sum <- sum + value
  }
  
  sum
}

library(tictoc)
tic()
y <- slow_sum(1:10)
toc()

5.032 sec elapsed

Parallelising map-reduce calls

Now suppose we have four sets of numeric vectors, in a list, and we want to calculate slow_sum() for each:

xs <- list(1:10, 11:20, 21:30, 31:40)

We could run lapply() over this, but it takes a while as it handles each list item in turn:

tic()
ys <- lapply(xs, slow_sum)
toc()

20.139 sec elapsed

Setting up for parallel processing

The future.apply package comes to the rescue!

The first step is to make a cluster from the available cores.

To parallelise on a local machine, use multisession in plan():

library(future.apply)
plan(multisession)

The default number of workers is availableCores().

We’ll also use the tictoc package for timings:

library(tictoc)

Using `future_lapply()`

future_lapply() is a drop-in parallel replacement for lapply()

plan(multisession, workers = 4)

tic()
ys <- future_lapply(xs, slow_sum)
toc()

5.266 sec elapsed

The four slow sums are calculated in about the same time as it takes to calculate one, since they are being calculated simultaneously on separate cores.

Your turn!

The efficient package contains a function to simulate a game of snakes and ladders, returning the number of rolls required to win.

remotes::install_github("csgillespie/efficient",
                         INSTALL_opts = "--with-keep.source")

Parallelise the following code:

library(efficient)
N <- 100
nrolls <- sapply(seq_len(N), snakes_ladders)

Use tictoc to compare the run-times. Roughly how large does N have to be for the parallel version to be worth using?

General Principles

Try to use vectorized functions where possible.
Otherwise use the apply family (and parellelise if necessary). Custom functions will often be useful here to pass to apply etc.
Try to keep for loops for true iterative computations or tasks that are fast in any case (optimizing code takes time!)

End matter

References

Good references on optimizing R code:

Wickham, H, Advanced R (2nd edn), Improving performance section, https://adv-r.hadley.nz/perf-improve.html
Gillespie, C and Lovelace, R, Efficient R programming, https://csgillespie.github.io/efficientR/

Tutorials on the Futureverse:

https://www.futureverse.org/tutorials.html

License

Licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License (CC BY-NC-SA 4.0).

Efficient Programming

Overview

Memory management

Overview

Basic data structures

Big Data

Growing Objects

Copy-on-Change

Benchmarking

Benchmarking

bench::mark()

Plotting benchmarks

Scaling

bench::press()

Exercise 1

Improving run time

Faster common operations

For loops

Vectorization

Recycling

ifelse()

Logical operations

Vectorization and Matrices

Matrices and recycling: rows

Matrices and recycling: columns

apply()

lapply()

sapply() and vapply()

Row/Column-wise Operations

Exercise 2 (h/t Raju Bhakta)

Exercise 2 (continued)

Parallelisation

Parallelisation

Example setup

Parallelising map-reduce calls

Setting up for parallel processing

Using future_lapply()

Your turn!

General Principles

End matter

References

License

`bench::mark()`

`bench::press()`

`ifelse()`

`apply()`

`lapply()`

`sapply()` and `vapply()`

Using `future_lapply()`